
PINS website
Exploring the Implications of Periodic Temporal Patterns in String Theory: A Shift from Particulate to Temporal Vibrational Correspondences

In the realm of string theory, where distinct vibrational frequencies traditionally correspond to specific particle types. String vibrations might alternatively correspond to periodic temporal patterns, similar to those observed in time crystals. This research seeks to either identify existing frameworks that contemplate such temporal vibrational correspondences and endeavor to develop a formal theoretical groundwork to integrate the concepts of time crystals with string theory, thereby proposing a paradigm shift from a purely particulate interpretation of string vibrations to one encompassing intrinsic temporal periodicity.
String Time Crystal Theory represents a groundbreaking synthesis of string theory’s multidimensional vibrational modes and the revolutionary idea of time crystals, which exhibit periodic motion in their lowest energy state, thereby spontaneously breaking time-translation symmetry. This advanced theoretical framework not only challenges our conventional understanding of space-time and matter but also proposes a novel phase of matter that integrates the complex mathematics of vibrating frequency domains from both theories into a cohesive scientific paradigm.
String Time Crystal Theory starts with the recognition that string theory represents a profound extension of local quantum field theory, offering a unified description of all interactions, including quantum gravitoelectromagnetism.
Foundations in String Theory and Quantum Mechanics
String theory extends the principles of local quantum field theory by positing that the universe’s most fundamental constituents are not point particles but minuscule strings. These strings’ vibrational modes correspond to various particles, a concept deeply rooted in complex mathematical formulations involving geometry, topology, and algebra. The vibrational frequencies of these strings, dictated by the Polyakov action, generate the observable particle spectrum and interactions in the universe.
Time Crystals: Breaking Symmetry in Time
Introduced by Frank Wilczek, time crystals conceptualize a state of matter that defies the time-translation symmetry inherent in classical physics. This phase exhibits periodic motion in its ground state, analogous to the spatial periodicity in crystal lattices. The Hamiltonian describing such systems incorporates non-static terms, leading to the spontaneous symmetry breaking in time and resulting in the time crystal’s periodic “ticking.”

Polyakov Action
In string theory, the fundamental objects are one-dimensional strings whose dynamics in spacetime are described by the Polyakov action or the Nambu-Goto action, leading to the equations of motion and constraints that govern how these strings evolve.
S_{\text{Polyakov}} = -\frac{T}{2} \int d^2\sigma \sqrt{-h} h^{ab} \partial_a X^\mu \partial_b X_\mu \eta_{\mu\nu}The vibrational modes of these strings, according to standard string theory, correspond to various particles observed in nature, with the mode’s frequency related to the particle’s mass and type. This is a spatial consideration, focusing on how strings extend and vibrate through space [1][2].
In metastring theory, the Polyakov action is reinterpreted within the framework of modular spacetime. Instead of treating spacetime as a fixed background, metastring theory introduces a generalized phase space where spacetime and momentum-space symmetries coexist. The Polyakov action incorporates Born reciprocity, emphasizing the duality between spacetime and energy-momentum space, fundamentally altering how strings are conceptualized.
S_{\text{Polyakov}}^{\text{modular}} = \frac{T}{2} \int d^2\sigma \left( \partial_a X^\mu \partial_b P_\mu - \frac{1}{2} h^{ab} (\partial_a X^\mu \partial_a X_\mu + \partial_a P^\mu \partial_a P_\mu) \right)
In this formulation, the modular Polyakov action introduces T-duality as a linearized symmetry, linking compactifications at radius RRR with those at radius 1/R1/R1/R, and integrates Born geometry, which unifies spacetime and momentum-space into a single mathematical structure. This provides a more dynamic interpretation of string vibrations, where both spatial and momentum fluctuations are equally fundamental.
Furthermore, metastring theory introduces the concept of relative locality, where spacetime structures and causal relations depend on an observer’s energy and momentum. This framework suggests that vibrational modes of strings are not limited to spatial dimensions but are deeply connected to periodic structures in time, aligning with the periodicity observed in time crystals and the discrete layering of modular spacetime.
The metastring perspective extends the vibrational analysis of strings to consider not only spatial frequencies but also temporal frequencies, bridging string dynamics with the periodic structures modeled in the Metastring Time Crystal framework. This connection enriches the study of quantum states, symmetries, and their manifestations across both spacetime and momentum-space.
By unifying traditional and modular formulations of the Polyakov action, metastring theory provides a broader framework for understanding quantum spacetime and how it relates to the dynamic evolution of strings [Freidel et al., 2017].
Integrating Temporal Patterns
To integrate the concept of time crystals, which exhibit periodic structure not in space but in time, we propose an extension to the string theory action to include terms that would favor solutions exhibiting temporal periodicity. This means looking for solutions to the string equations of motion that are not only stable configurations in space but also in time—leading to a breaking of time-translation symmetry without the input of external energy, akin to the ground state of a time crystal.
S_{\text{extended}} = S_{\text{Polyakov}} + \int d^2\sigma V(\sigma, X^\mu)The extension proposed here introduces V(σ,Xμ), a potential function added to the traditional Polyakov action. This term is meant to encapsulate the effects of temporal periodicity—akin to those observed in time crystals—on the strings’ dynamics. Time crystals are phases of matter that exhibit periodic structure not in space, as regular crystals do, but in time, leading to a repeating pattern that persists without external energy input.
Incorporating V into the action aims to explore whether string theory can be extended to describe not just the particles of the universe but also novel temporal phenomena that could emerge from the strings’ interactions with a time-crystalline field or background. This approach suggests a broader framework in which the fundamental strings of the universe exhibit complex dynamics, influenced by both their traditional spatial vibrations and new types of temporal patterns.
This extended action invites investigation into how such temporal patterns might influence the properties of the particles that strings represent, potentially leading to new insights into the nature of matter, energy, and the fabric of spacetime itself.
String theory’s mathematical framework, particularly the Polyakov action, could describe the Brownian motion of quantum states in microtubules within neurons. There are parallels between the 25 quantum states in microtubules and the dimensions required for consistent string theory, proposing that string theory might explain quantum neurobiological phenomena, including consciousness. (Varshovi 2024)
Synthesis: String Time Crystal Theory in the Vibrating Frequency Domain
String Time Crystal Theory emerges from intertwining the vibrational dynamics of string theory with the temporal periodicity of time crystals. This synthesis could be explored through a combined action S=SPolyakov+Sext, integrating the Polyakov action with a term Sext representing time crystal behavior, including a periodic potential V that models the time crystal’s structure potentially influenced by string theory’s extra dimensions.
The Lagrangian’s interaction terms might showcase couplings between the string’s vibrational frequencies (ω) and the periodic field ϕ symbolizing the time crystal, expressed as Linteraction=g(ω,ϕ)cos(ωt+θ)ϕ(t), where g(ω,ϕ) indicates the coupling strength, and θ a phase offset.
Quantizing this action could unveil a quantized spectrum of vibrational frequencies, reflecting the spatial properties of strings and the temporal periodicity inherent in time crystals. This leads to a novel phase of matter characterized by both spatial and temporal order, a significant departure from traditional phases known in physics.
Practical application
The realization of string time crystal is a hot topic, recently explored by research team in Delft and Brown Universities. Graphene Nanotubes (GNTs) have also been proposed as a viable material for creating nanostring time crystals in room temperature. Read more at: https://nanostring.wordpress.com/
Conclusion
String Time Crystal Theory proposes a framework that combines the rich, multidimensional structure of string theory with time crystals. By extending our understanding of symmetry breaking into the temporal domain and integrating it with the vibrational dynamics of strings, this theory explains the nature of spacetime, matter, and the fundamental forces of the universe. Rigorous mathematical analysis and computational simulations support the implications and applications of this innovative theory.
References
- Wilczek, F. (2012). Quantum Time Crystals. arXiv:1202.2539v2 [quant-ph]. Retrieved from https://arxiv.org/abs/1202.2539
- Shapere, A., & Wilczek, F. (2012). Classical Time Crystals. arXiv:1202.2537v2 [cond-mat.other]. Retrieved from https://arxiv.org/abs/1202.2537
- Gross, D. J. (1996). The Role of Symmetry in Fundamental Physics. Proceedings of the National Academy of Sciences, 93(25), 14256-14259. DOI: 10.1073/pnas.93.25.14256
Exploring the Horizon: Unveiling Stringy Physics Beyond Quantum Mechanics
In the ever-evolving quest to understand the fundamental forces of nature, a groundbreaking study by Donatello Dolce at the University of Camerino has unveiled a novel approach that transcends traditional quantum mechanics. Titled “New Stringy Physics beyond Quantum Mechanics from the Feynman Path Integral,” this research offers a fresh perspective on elementary particle dynamics, promising to reshape our understanding of the universe.
Redefining Quantum Particle Dynamics
Dolce’s study delves deep into the Feynman Path Integral, a cornerstone of modern physics, to reveal an uncharted territory of elementary quantum particle dynamics. By investigating this integral, Dolce uncovers that the dynamics of elementary particles are intricately linked to compact (cyclic) world-line parameters, which act as an internal clock implicit in conventional undulatory mechanics. This revelation lays the foundation for a new four-dimensional stringy description of elementary particles, potentially marking a significant leap beyond the realms of quantum mechanics.
Quantum Mechanics from a Novel Lens
The innovative approach posits that quantum mechanics originates from a non-trivial compact nature of Minkowskian space-time. This perspective is not only a testament to the Elementary Cycles Theory (ECT), which has consistently aligned with known physics across various fields but also provides compelling conceptual support for a unified scenario of quantum and relativistic physics. The research suggests that the first glimpses of this new physics, characterized by ultra-fast cyclic time dynamics, will be observable through quantum phenomena with experimental time accuracy in the order of 10^-21 seconds.
A New Framework for Elementary Particles
Dolce’s formulation introduces Elementary Cycle String Theory (ECST), where elementary particles are envisioned as strings within a four-dimensional Minkowskian space-time, eliminating the need for extra dimensions typical in traditional string theory. This model is both phenomenologically predictive and falsifiable, devoid of fine-tunable parameters or hidden variables, potentially offering a deterministic view of quantum mechanics.
Implications and Future Directions
The implications of this research are profound, suggesting new physics will be uncovered by investigating quantum phenomena with unprecedented time precision. It challenges conventional quantum mechanics and invites the scientific community to rethink the fundamental principles that govern our universe.
As we stand on the brink of a new era in theoretical physics, Dolce’s work not only enriches our understanding of the quantum realm but also lights the path toward unifying the quantum and relativistic descriptions of nature. The journey to decipher the mysteries of the universe continues, with “New Stringy Physics beyond Quantum Mechanics” promising to be a cornerstone in the quest for a deeper, more coherent understanding of the cosmos [3].
Unlocking the Secrets of Time: The Classical Physics Behind Quantum Time Crystals

In the mysterious and often counterintuitive world of quantum mechanics, the concept of time crystals has emerged as a fascinating phenomenon. Unlike ordinary crystals, which display a repeating pattern in space, time crystals exhibit a repeating pattern in time, offering a new dimension of periodicity in the laws of physics. Originally theorized by Frank Wilczek in 2012, time crystals have captivated scientists with the possibility of matter spontaneously exhibiting time-periodic motion. This notion challenges our classical understanding of phase transitions and opens the door to exploring the fundamental nature of time itself.
Recent advancements in numerical simulations have provided intriguing insights into the nature of time crystals, particularly those known as prethermal time crystals. Researchers from the University of Cambridge, UK, and the University of California, Berkeley, have discovered that certain types of these enigmatic structures can be described using classical physics. This groundbreaking finding suggests that the complex quantum effects previously thought to be essential for the stabilization of time crystals may not be necessary after all.
The significance of this discovery lies in its potential to simplify the theoretical and experimental investigation of time crystals. By demonstrating that classical equations of motion can capture the essential features of quantum time crystals, these studies open new avenues for exploring these phenomena in systems that are more accessible and easier to control. Furthermore, the realization that prethermal time crystals can arise from classical dynamics challenges the conventional wisdom that quantum fluctuations are crucial for their existence.
The implications of these findings extend beyond the realm of theoretical physics. By uncovering the classical roots of quantum time crystals, scientists may unlock new strategies for creating these structures in the laboratory. The research also raises profound questions about the nature of time and the potential for discovering other exotic phases of matter that transcend the traditional boundaries of space and time.
As we stand at the frontier of this exciting field, the journey to fully understand and harness the potential of time crystals is just beginning. The classical view of quantum time crystals not only enriches our understanding of the quantum world but also highlights the universality of the physical laws that govern our universe [4].
Exploring Time as a New Dimension: The Emergence of Quantum Time Crystals

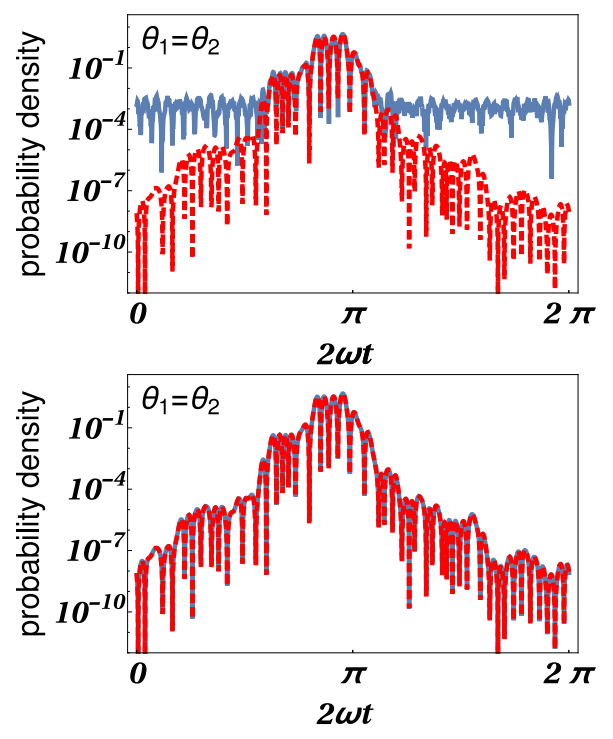
Red dashed lines represent probability densities for detecting two atoms at θ1 = θ2 versus time for an eigenstate of the effective Hamiltonian with E = 616, λ = 600, and k0 = 100, while blue solid lines show the probability density for the corresponding Floquet eigenstate of the full Hamiltonian with ω = 104 (top panel) and ω = 3 × 105 (bottom panel).
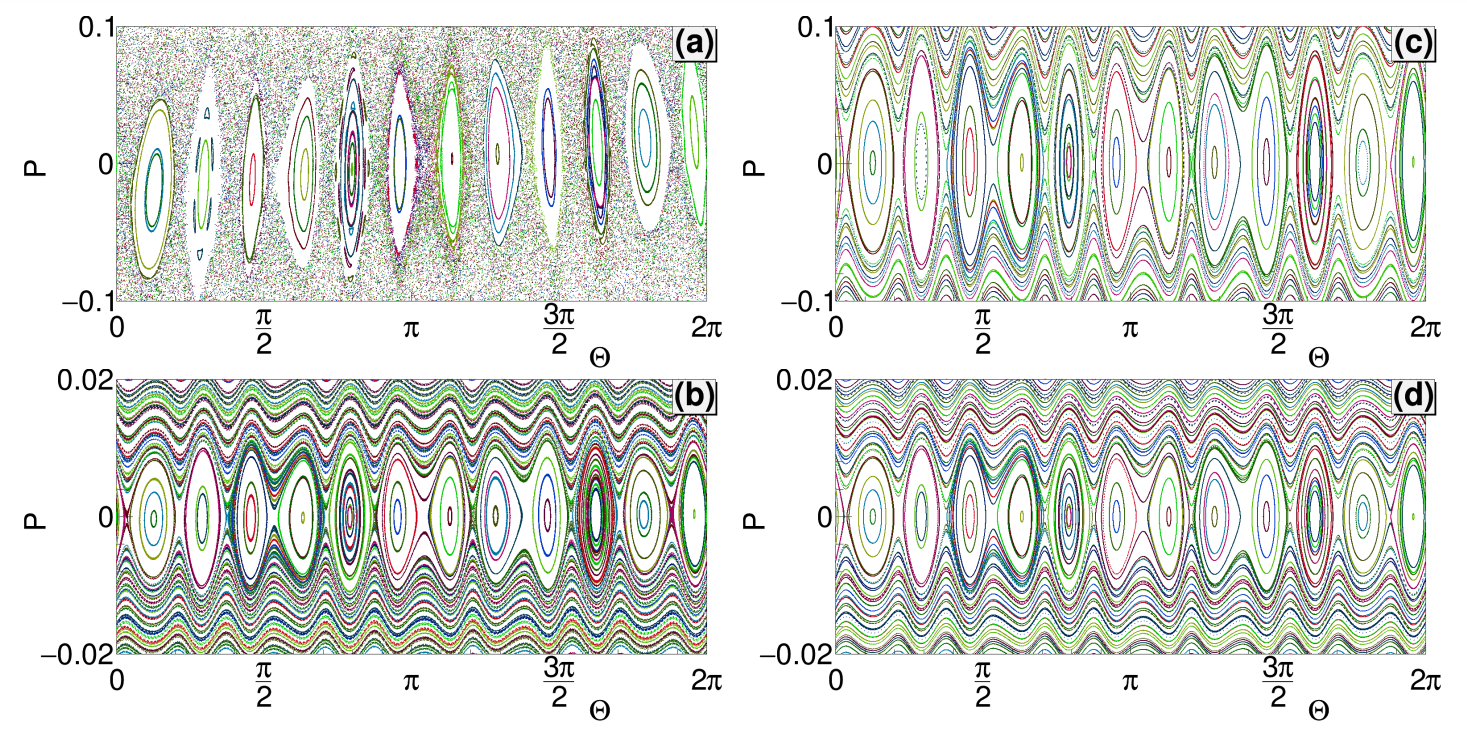
In the realm of quantum physics, the notion of time crystals introduces a fascinating twist to our understanding of matter. These unique quantum many-body systems, through interactions between particles, exhibit the extraordinary ability to self-organize their motion in a periodic manner over time. This spontaneous formation of temporal structures draws a parallel with how crystals in solid-state physics arrange themselves spatially. The research led by Krzysztof Giergiel, Artur Miroszewski, and Krzysztof Sacha at the Jagiellonian University in Kraków, Poland, dives into this intriguing concept, showcasing how time crystals, or more specifically, prethermal time crystals, can be simulated in quantum systems.
A striking feature of time crystals is their emergence not from equilibrium but through non-equilibrium dynamics, a realization that pivots away from the original propositions by Frank Wilczek in 2012. This phenomenon, known as “discrete time crystals,” illustrates a breaking of discrete time translation symmetry, where a system, under periodic driving, exhibits motion that reorganizes itself to oscillate with a period distinct from that of the external drive.
Giergiel and his colleagues extend this concept further by demonstrating that time crystals can mimic properties of space crystals when subjected to periodic driving. This approach allows for the exploration of phenomena like Anderson localization and many-body localization in the time domain, providing a new lens through which to understand and manipulate quantum systems.
One of the study’s pivotal findings is the realization that classical mechanics can effectively describe certain aspects of quantum time crystals. Through numerical simulations, the team illustrates how a classically driven system can replicate the behavior of its quantum counterpart, offering insights into the formation of quasi-crystal structures in time. This classical description significantly simplifies the theoretical framework for time crystals, broadening the possibilities for experimental realization and study.
In essence, the research opens up a fascinating territory where time itself becomes a dimension for exploring condensed matter physics. It challenges our conventional understanding and offers a novel perspective on the dynamics of quantum systems. Through the manipulation of periodic driving, the study hints at the potential to engineer systems that exhibit exotic interactions, shedding light on the rich interplay between time, quantum mechanics, and the fundamental nature of matter [5].
Expanding the Horizons of Quantum Field Theory: A Dive into Higher-Dimensional Liouville Theory

Quantum Field Theory (QFT) has long been a cornerstone of theoretical physics, providing a framework to describe the quantum mechanics of fields and particles. Traditionally confined to lower dimensions due to mathematical and physical constraints, recent research has broken new ground by extending the Liouville Conformal Field Theory (LCFT) into higher dimensions, offering fresh insights and potential breakthroughs in understanding the fabric of the universe.
In a groundbreaking paper titled “Liouville Conformal Field Theory on the higher-dimensional sphere,” Baptiste Cerclé at the University of Helsinki has meticulously crafted a higher-dimensional framework for LCFT, which historically has been challenging due to the complex nature of conformal geometry beyond two dimensions. This innovative approach not only generalizes the foundational principles laid out by Polyakov in 1981 but also integrates recent advancements in conformal geometry, thereby expanding the scope of LCFT to encompass even-dimensional spheres.
From Two to Many: A Leap into Higher Dimensions
LCFT, initially formulated for two-dimensional spaces, relies on the summation over Riemannian metrics on surfaces to describe quantum gravity. Cerclé’s work ingeniously adapts this to higher dimensions, utilizing advanced mathematical constructs such as GJMS operators and Q-curvature to preserve the theory’s conformal nature. This adaptation is not merely a theoretical exercise; it has profound implications for the study of quantum geometry and potentially for string theory and the AdS/CFT correspondence, which posits a relationship between gravity in Anti-de Sitter space and conformal field theories.
A Quantum Leap for Physics
The extension of LCFT into higher dimensions is a monumental stride towards unifying various branches of physics. It opens new avenues for exploring quantum phenomena in higher-dimensional spaces, potentially leading to a deeper understanding of the universe’s fundamental structure. Furthermore, this research enriches the dialogue between mathematics and physics, demonstrating how advanced mathematical techniques can lead to significant breakthroughs in theoretical physics.
Future Directions and Implications
Cerclé’s work sets the stage for further explorations into higher-dimensional quantum field theories. The potential for discovering new quantum states of matter, understanding the fabric of spacetime, and even unraveling the mysteries of dark matter and dark energy is immense. As researchers continue to build on these foundational insights, the boundary between the known and the unknown continues to expand, promising exciting new discoveries in the realms of quantum physics and cosmology [6].
References
[1] https://en.wikipedia.org/wiki/Polyakov_action
[2] Polyakov, A.M. (1981). Quantum Geometry of Bosonic Strings. Physics Letters B, 103(3), [Pages]. L.D. Landau Institute for Theoretical Physics, Moscow, USSR. Received 26 May 1981.
[3] Dolce, D. (2022). New Stringy Physics beyond Quantum Mechanics from the Feynman Path Integral. University of Camerino. arXiv:2106.05167v4 [physics.gen-ph].
[4] Engelhardt, G. (2021). A Classical View of Quantum Time Crystals. Physics, 14, 132. DOI: 10.1103/Physics.14.132
[5] Giergiel, K., Miroszewski, A., & Sacha, K. (2018). Time crystal platform: From quasi-crystal structures in time to systems with exotic interactions. arXiv:1710.10087v3 [cond-mat.quant-gas].
[6] Cerclé, B. (2019). Liouville Conformal Field Theory on the higher-dimensional sphere. University of Helsinki. arXiv:1912.09219v1 [math.PR].

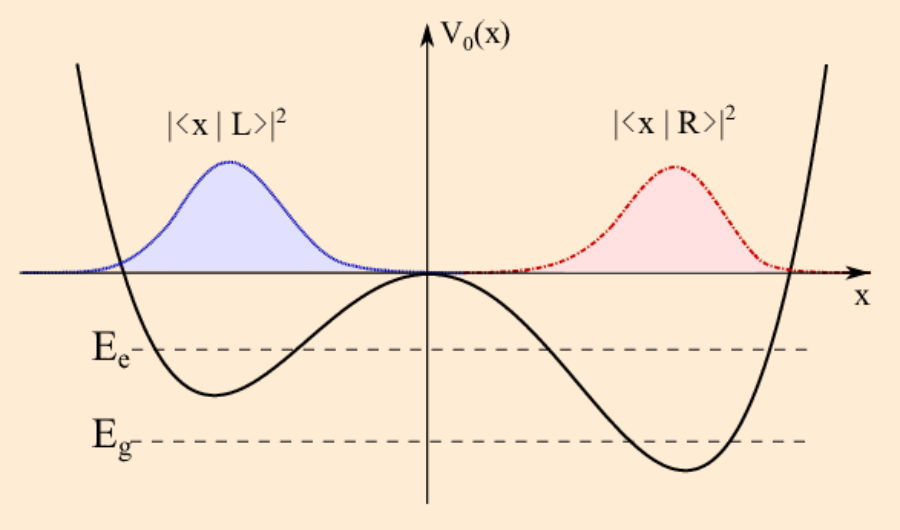
Superstring Time Crystal & Schrödinger Equation
Superstring time crystal combined with the Schrödinger equation introduces a fascinating interdisciplinary idea that merges three pivotal areas of physics: superstring theory, the notion of time crystals, and the principles encapsulated by the Schrödinger equation. Superstring theory suggests a model where all fundamental forces and particles are described as tiny, vibrating strings within a higher-dimensional space, implying extra dimensions that are compactified. Time crystals represent a phase of matter characterized by a perpetual oscillation or periodic motion in time, achieved without external energy or loss. The Schrödinger equation, a fundamental equation in quantum mechanics, dictates the behavior of quantum systems through a wave function.
The idea of integrating Superstring Time Crystal and Schrödinger Equation posits a theoretical model capable of describing the behavior and energy spectrum of superstring systems that exhibit regular, self-repeating patterns over time. This model shows a system with discrete energy levels and challenges conventional understanding by potentially violating energy conservation principles. It would also exhibit exotic features such as stability against disruptions, quantum entanglement, and a blend of continuous and discrete time symmetries.
This idea ventures into the quantum physics and mathematics, encompassing theories like supersymmetry, conformal field theory, and quantum chaos. Researchers have proposed models exploring its feasibility, highlighting the complexity and interdisciplinary challenge it presents. This inquiry into the confluence of superstring theory, time crystals, and the Schrödinger equation underscores the ongoing exploration and theoretical experimentation in advanced physics.
Exploring Wavefunctions and Schrödinger’s Cat in String Theory
A wavefunction in quantum mechanics is a fundamental concept that represents the quantum state of a system, like a particle or, in the realm of string theory, a vibrating string. This mathematical function assigns a complex number, or amplitude, to every possible state of the system. The probability of the system being found in any given state upon measurement is determined by the square of this amplitude.
Schrödinger’s cat states introduce the notion of quantum superposition into this framework. Named after Erwin Schrödinger’s thought experiment, these states illustrate how a quantum system can simultaneously exist in multiple, distinct states. For instance, a particle could be in two places at once. The famous analogy involves a cat that is both alive and dead until observed, tied to a mechanism triggered by the decay of a radioactive atom.
In string theory, these concepts are extended to describe the properties of strings, tiny one-dimensional objects that form the fabric of the universe. Here, a wavefunction would describe not just the position or momentum of a string but its various vibrational modes – its energy, mass, charge, and frequency. Strings can also exhibit superposition, being in multiple states simultaneously, such as different vibrational modes or even as different fundamental particles.
These ideas challenge our classical intuition and open up new avenues for understanding the quantum underpinnings of reality, where particles are replaced by strings, and certainty is replaced by probabilities. For those intrigued by the intersection of quantum mechanics and string theory, further exploration into wavefunctions and Schrödinger cat states offers a glimpse into the theoretical framework attempting to unify all fundamental forces of nature.
Understanding Wave Function Collapse in String Field Theory, String Time Crystals, and Superstring Time Crystals
Wave function collapse in quantum mechanics is the phenomenon where a quantum system transitions from being in multiple states at once (a superposition) to a single state upon observation. This concept takes on new dimensions within string field theory, where the wave function describes the quantum states of strings spread across space and time. These strings are not just simple particles but oscillating entities that can have various configurations, each with its own amplitude and phase in the theory’s mathematical framework.
In the context of string theory, we encounter the intriguing concepts of string time crystals and superstring time crystals. A string time crystal represents a theoretical system in which strings manifest periodic behavior over time, effectively breaking the symmetry of time translation in a predictable, clock-like pattern. This idea is further expanded in superstring time crystals, which incorporate the complexities of superstring theory, including extra spatial dimensions and supersymmetry, suggesting an even richer tapestry of temporal periodicity and quantum states.
The discussion of wave function collapse within these contexts is speculative and represents a frontier in theoretical physics and mathematics. It intersects with advanced concepts such as supersymmetry, conformal field theory, the AdS/CFT correspondence, and quantum chaos. Despite the fascinating theoretical frameworks proposed, the existence of string time crystals, superstring time crystals, and the precise nature of wave function collapse in these systems remains unproven and largely hypothetical. Theoretical models and scenarios have been suggested by researchers, but these ideas are still on the fringes of mainstream scientific acceptance and understanding.
The exploration of wave function collapse in string field theory, along with the hypothetical existence of string and superstring time crystals, challenges and expands our understanding of quantum mechanics and the fundamental structure of the universe. These concepts push the boundaries of theoretical physics, inviting further research and debate in the quest to unify the laws of nature. For those intrigued by the possibilities of string theory and its implications for quantum mechanics, the journey into these speculative realms offers a glimpse into the potential future directions of fundamental physics.
