References
Carroll, S. M., Hoffman, M., & Trodden, M. (2003). Can the dark energy equation-of-state parameter w be less than -1? Physical Review D, 68(2), 023509. https://doi.org/10.1103/PhysRevD.68.023509
Haroche, S., & Raimond, J.-M. (2006). Exploring the Quantum: Atoms, Cavities, and Photons. Oxford University Press.
Wilczek, F. (2012). Quantum time crystals. Physical Review Letters, 109(16), 160401. https://doi.org/10.1103/PhysRevLett.109.160401
Else, D. V., Bauer, B., & Nayak, C. (2020). Discrete time crystals. Annual Review of Condensed Matter Physics, 11(1), 467-499. https://doi.org/10.1146/annurev-conmatphys-031119-050658
Bouhmadi-López, M., Kiefer, C., & Martín-Moruno, P. (2019). Phantom singularities and their quantum fate: general relativity and beyond—a CANTATA COST action topic. General Relativity and Gravitation, 51, Article 135. https://doi.org/10.1007/s10714-019-2618-y
Quantum Phantom Energy Framework
Quantum Phantom Energy is a theoretical framework that merges principles from quantum mechanics and cosmology, suggesting an exotic form of energy that could drive perpetual oscillations and non-classical behavior in quantum systems, linked to dark energy’s mysterious properties (Carroll et al., 2003; Haroche & Raimond, 2006). Quantum Phantom Energy hypothesizes a bridge between observed cosmic expansion driven by dark energy and stable, low-energy oscillatory states seen in quantum systems, such as quantum time crystals (Wilczek, 2012; Else et al., 2020). This idea aligns with research on phantom singularities in general relativity, exploring possible quantum fates of cosmic phenomena (Bouhmadi-López et al., 2019).
Quantum Oscillators and Phantom Energy
Quantum harmonic oscillators are a foundational model in quantum mechanics, illustrating systems with discrete energy levels. Phantom energy, a theoretical form of dark energy, is postulated to drive cosmic expansion at a rate that could lead to a “Big Rip” in the distant future. Integrating quantum oscillators with phantom energy suggests that high-energy, non-classical states may play a role in cosmic phenomena or in energy transfer at the quantum level. These oscillators could embody phantom energy’s dynamics, behaving in ways that challenge classical interpretations.
Quantum Polar Energy Oscillators in M-Theory and String Theory
In string and M-theory, the universe’s particles and forces emerge from different vibrational modes of one-dimensional “strings” or higher-dimensional “branes.” A quantum polar energy oscillator in these frameworks could describe energy distributed among specific vibrational modes. This interpretation aligns with the harmonic oscillator model, which governs these vibrational states’ quantized nature. It’s possible that oscillatory modes in strings and branes capture phantom energy-like behavior, reflecting energy exchanges within the “quantum foam” of spacetime.
Quantum Many-Body Scars
Quantum many-body scars represent special nonthermal states that defy the usual spread of quantum entanglement, retaining coherence over extended periods. They offer a glimpse into how stable, low-entanglement states can exist within complex quantum systems, making them uniquely resilient. This stability and resistance to thermalization in many-body scars may help conceptualize how phantom energy could interact with large-scale quantum systems. Observed in Rydberg atom arrays, these scars suggest a unique form of vibrational or “phantom-like” energy that remains conserved and could provide insights into maintaining coherence in quantum systems.
Quantum Time Crystals
Quantum time crystals break time-translation symmetry, causing oscillations in their lowest energy state. They exhibit sustained, periodic motion at zero net energy, resonating with the idea of phantom energy as a source that could potentially perpetuate motion without conventional energy input. Time crystals could metaphorically represent “phantom oscillations,” suggesting how a low-energy quantum state might hold consistent oscillatory motion, similar to the continuous expansion driven by phantom energy on a cosmological scale.
Interconnected Concepts
- Phantom Energy and Quantum Scars: Phantom energy might be likened to the missing kinetic energy in high-momentum atoms observed in quantum scars. Similarly, in M-theory, energy could be “scarred” or retained in specific vibrational patterns, existing in nonthermal states akin to the stability seen in many-body scars.
- Resonance with Quantum Time Crystals: The persistent oscillations in quantum time crystals align with the harmonic oscillations of strings and branes in M-theory. If phantom energy behaves as hypothesized, it could drive perpetual, low-energy oscillations within quantum systems, sustaining resonance within an M-theory framework.
- Experimental Verification: Experiments with quantum many-body scars in various settings could reveal how brane vibrations distribute phantom-like energy modes. Exploring scars in other quantum systems may also provide clues about how this phantom energy might interact with observable matter.
- Theoretical Models: Creating models that incorporate both phantom energy in non-classical states and the periodicity of time crystals might bridge these ideas. Such models could also suggest applications in quantum technology, including energy conservation, stable quantum states, and novel information storage solutions.
- Exploring these connections might offer new perspectives on the fundamental principles of quantum mechanics, dark energy, and cosmology, opening pathways for innovative quantum technologies and theoretical advancements.
String Time Crystal Theory ~ Quantum Tokenisation
Efficient data processing:
Quantum Intelligence (QI) can handle quantum tokenisation of large and complex data sets more efficiently than classical AI. This is particularly significant in natural language processing (QNLP) tasks, where tokenisation is a critical step for quantum algorithms. By leveraging quantum algorithms to process and analyze qubit data at unprecedented speeds, Quantum Intelligence improves the performance of generative quantum QNLP models. This has profound implications for String Time Crystal and Quantum Intelligence, where token structuring supports advanced simulations and predictive models within String Time Crystal Theory ~ Quantifiers Tokenisation frameworks.
In Quantum Intelligence, the quantifiers tokenisation is crucial for processing interactions in complex databases. Quantum Tokenisation breaks down data into manageable units, making it essential for quantum natural language processing. Quantum algorithms dramatically enhance this process, increasing the accuracy, quality, and efficiency of generative models. This is particularly relevant to the String Time Crystal Theory ~ Quantifiers Tokenisation, where the quantum processing of data enhances the ability to predict and simulate novel quantum states, accelerating discoveries in physics.
String Time Crystal Theory ~ Quantifiers Tokenisation:
String Time Crystal Theory applies String Theory and Quantum Intelligence to explore periodic motion in time, breaking translational-time symmetry. Central to this theory is quantifiers tokenisation, where understanding quantum tokens enables simulations of new states of matter. These tokens, processed by Quantum Intelligence, evolve into generative models that offer breakthroughs in modeling complex quantum phenomena, such as multiverses, while also enhancing our understanding of the laws governing space and time.
Quantum Tokenisation and Axion Time Crystal Theory:
Incorporating axions—hypothetical particles linked to dark matter—into Axion Time Crystal Theory expands our understanding of time crystals. These structures, periodic in both time and space, are more efficiently modeled with Quantum Intelligence. Quantum Tokenisation plays a crucial role in simulating these complex systems, allowing for deeper insights into axions and their potential impact on the universe. By tokenizing the data into manageable quantifiers, Quantum Intelligence enables more precise modeling than traditional approaches.
Quantum Intelligence and Quantum Tokenisation:
Quantum Intelligence combines distributed quantum computation with generative AI, allowing for more efficient problem-solving, particularly for predictive models. Quantum Tokenisation is a key element in this process, enabling faster simulations and modeling in areas such as String Time Crystal Theory. Quantum neural networks (QNNs), powered by Quantum Intelligence, handle large data sets, creating opportunities for breakthroughs in time crystal research and string theory simulations. Quantum Tokenisation enhances the ability to explore and simulate multiverses and quantum phenomena, opening new frontiers in quantum physics research.
String Time Crystal Theory:
The String Time Crystal Theory describes how the phantoms in a string exhibit periodic motion in time, breaking translational-time symmetry. This is similar to a string vibrating in a specific pattern that repeats itself in time, much like a crystal structure in space, but in the dimension of time. Using the principles of string theory, these phenomena can be studied to gain insight into the fundamental nature of time and matter.
Quantum Tokenisation:
In this context, quantum tokenisation is used to break down complex data about a string time crystal into manageable units (tokens). These tokens represent specific states or configurations of the string in time. Quantum algorithms that process these tokens at unprecedented speeds enable efficient analysis and simulation of the behavior of a string time crystal.
Example:
Consider a string time crystal model in which the string is a closed loop with several interaction points (vertices). Each vertex represents a point at which the state of the string can change under the influence of quantum mechanics. By tokenising the data from this model, each token can represent a specific configuration of the string at a given time.
Using quantum algorithms, these tokens can be rapidly processed to simulate the behavior of the string over time. This allows us to study how the string evolves, identify stable configurations, and understand the effects of different parameters on the dynamics of the string. This approach leads to identifications about the nature of time crystals and their potential applications in quantum computers and other fields.
References
[1] Zhu, Y., & Yu, K. (2023): Artificial intelligence for quantum and quantum for AI: Optical and Quantum Electronics, 55, 697; [2] KDnuggets. (2024): Breaking Down Quantum Computing: Implications for Data Science and AI: KDnuggets, February 7; [3] Sgarbas, K. N. (2007): The Road to Quantum AI: arXiv:0705.3360; [4] Widdows, D., Kitto, K., & Cohen, T. (2021): Quantum Mathematics in AI: Journal of AI Research, 72, 1307-1341; [5] Kozin, V. K., & Kyriienko, O. (2019): Quantum Time Crystals: Phys. Rev. Lett., 123, 210602; [6] Engelhardt, G. (2021): A Classical View of Quantum Time Crystals: Physics, 14, 132; [7] Zakrzewski, J. (2012): Crystals of Time: Physics, 5, 116; [8] Choi, K., & Righi, N. (2024): Axion Theory and Model Building: PoS COSMICWISPers, 039; [9] Pragmatic Coders. (2024): What is Quantum AI? Pragmatic Coders, September 27; [10] Wikipedia: Quantum Machine Learning: Wikipedia.
Holistic String Time Crystal Theory
Holistic Approach: Bridging String theory, Quantum Mechanics and Time Crystal Reality

The “Holistic String Time Crystal Theory” presents an innovative integration of quantum mechanics, general relativity, and holistic health principles to offer a unified understanding of the universe. This theory emphasizes the interconnectedness of physical, psychological, intellectual, neuronal, spiritual, and scientific health, all underpinned by the concept of Homo Quanticum Centrism. By exploring the intersection of the Rindler horizon from relativistic physics and the Heisenberg uncertainty principle from quantum mechanics, the theory highlights the challenges and paradoxes that emerge when these foundational principles collide, particularly under extreme conditions. The Holistic String Time Crystal Theory suggests that reality is shaped by an intricate web of cosmic and quantum influences, ultimately requiring a comprehensive approach to fully grasp the complexities of the universe. This holistic perspective bridges gaps in scientific understanding and offers a novel viewpoint on the relationship between consciousness, reality, and spacetime.
This section delves into the Holistic String Time Crystal Theory, which unites the foundational principles of string theory, quantum mechanics, and time crystal phenomena to offer a comprehensive view of the universe. By integrating string theory’s multidimensional frameworks with the probabilistic nature of quantum mechanics and the emergent properties of time crystals, this approach proposes a cohesive understanding that transcends conventional boundaries. The theory suggests that the universe operates on a deeply interconnected level, where the fabric of spacetime is woven with the threads of quantum fluctuations, string vibrations, and the crystalline structure of time itself. This holistic perspective unifies disparate scientific theories and underscores the importance of considering the universe as a dynamic, interconnected whole.
The Holistic Theory: A Unified View of the Universe
The Holistic Theory merges the principles of quantum mechanics with general relativity, aiming to present a unified and comprehensive understanding of the universe. The theory emphasizes several key areas:
- Physical and Psychological Health: Reflects the immense cosmic scales and spacetime curvature, acknowledging the complex relationship between mental and physical wellness.
- Intellectual & Consciousness Health: Highlights an all-encompassing view where the complex behaviors of quantum particles are intertwined. It positions Intellect and Consciousness as the fundamental pillars that support the Universe’s Information and Quantum Information Fields, laying the foundation for Homo Quanticum Centrism.
- Neuronal & Emotional Health: Stresses the vital role of the observer, suggesting that individual consciousness and emotions could significantly influence reality.
- Science and Spiritual Health: Aligns with the essence of Quantum Centrism, revealing the interconnection between Quantum Technology and Quantum Biology. It bridges the gap between scientific research and spiritual understanding, leading to a deeper appreciation of Intellectual and Emotional Consciousness.
The theory provides a holistic perspective on reality, highlighting the interdependent relationship between Physical, Psychological, Intellectual, Neuronal, Spiritual, and Scientific health, all encapsulated within the concept of Homo Quanticum Centrism.
The Rindler horizon represents a conceptual boundary in spacetime that differentiates regions observable by an observer who is constantly accelerating from those that are forever out of reach. This horizon, akin to the event horizon of a black hole, is not a consequence of the curvature of spacetime but is instead a result of the principles of special relativity. The idea originates from the work of Wolfgang Rindler, who explored the complexities of uniformly accelerating frames in a flat spacetime context [1].
In contrast, the Heisenberg uncertainty principle is a fundamental concept in quantum mechanics. It states that it’s impossible to simultaneously measure the exact position and momentum of a particle with absolute precision. The precision of one measurement inherently compromises the accuracy of the other. This principle ensures that the product of the uncertainties in position and momentum is always greater than a certain fixed value, which is closely related to Planck’s constant. This uncertainty principle is not exclusive to position and momentum but also applies to other pairs of conjugate variables such as energy-time and frequency-time [2].
[1] Wikipedia: Rindler coordinates
[2] Greg Egan, “The Rindler Horizon“
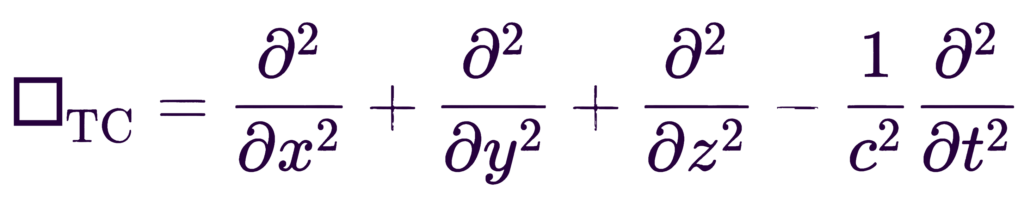
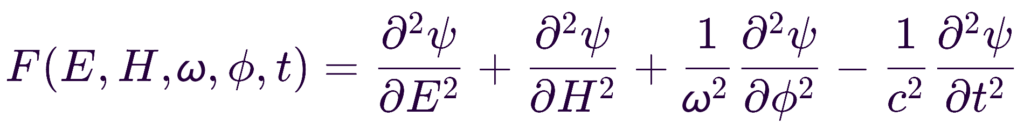
- E: Energy associated with the system.
- H: Hamiltonian, which represents the total energy operator in quantum mechanics (potentially time-dependent).
- ω: Frequency, related to the oscillatory nature of the wave.
- φ: Phase angle, which defines the position in the oscillatory cycle.
Time Operator
\frac{1}{c^2} \frac{\partial^2}{\partial t^2} : Represents the temporal evolution of the system, potentially with the energy and Hamiltonian influencing the time evolution. We could write this term as:
\frac{1}{c^2} \frac{\partial^2}{\partial t^2} \rightarrow \frac{\partial^2 \psi}{\partial E \, \partial H}Here, \frac{\partial^2 \psi}{\partial E \, \partial H} represents a coupling between energy and Hamiltonian as the total energy of the system, introducing both energy parameters in the time evolution.
Energy Operator
\frac{\partial^2}{\partial E^2} : Replaces one of the spatial derivative terms and accounts for changes with respect to energy.
Hamiltonian Operator
\frac{\partial^2}{\partial H^2} : Another term to replace a spatial derivative, accounting for changes with respect to the Hamiltonian (total energy of the system).
Frequency and Phase Operator
\frac{1}{\omega^2} \frac{\partial^2}{\partial \phi^2} : The oscillatory component, reflecting the dependence on frequency \omega and phase angle \phi.
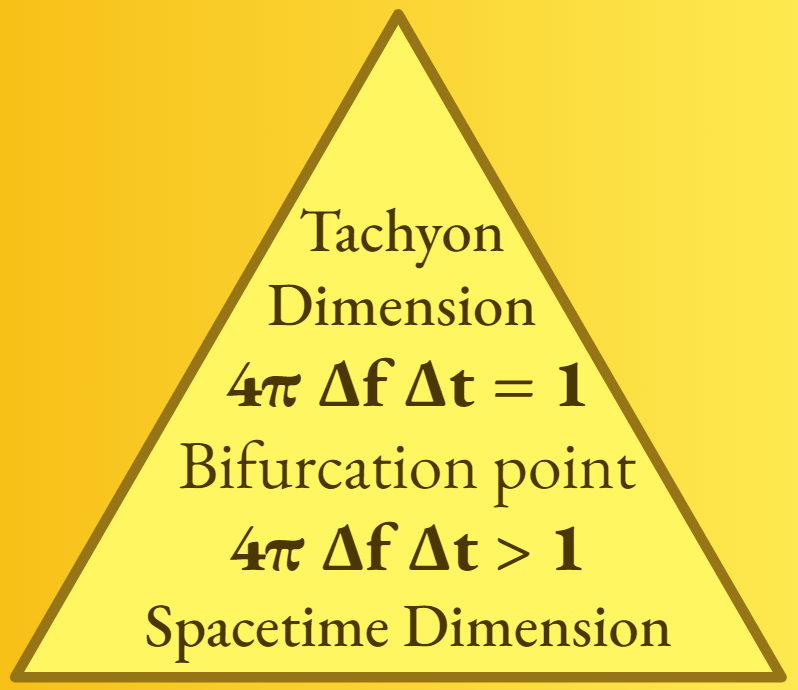
The intersection of the Rindler horizon concept from relativistic physics with the Heisenberg uncertainty principle from quantum mechanics presents some fascinating scenarios. Imagine an observer aboard a perpetually accelerating spaceship, moving away from a source emitting photons of constant frequency. Due to the Doppler effect, the observer will perceive these photons as increasingly redshifted, with their frequency decreasing as they approach the Rindler horizon. In this situation, any attempt by the observer to precisely determine the photon’s position and frequency encounters the Heisenberg constraint, represented by the formula ΔxΔf ≥ c/4π. This means that as the uncertainty in the frequency measurement decreases, the uncertainty in the position measurement increases, and vice versa. This inherent uncertainty prevents the accurate determination of the exact location of the Rindler horizon using photon measurements.
In a similar vein, consider an observer trying to measure the energy-time relationship of a particle as it approaches the Rindler horizon. Here, gravitational redshift would lead to a decrease in the observed energy of the particle as it gets closer to the horizon. Any measurement attempting to pinpoint the energy and time of the particle is constrained by the Heisenberg uncertainty principle, which in this context can be expressed as ΔEΔt ≥ ℏ/2 or equivalently, ΔfΔt ≥ 1/4π. As a result, a decrease in uncertainty in the energy or frequency measurement increases the uncertainty in the time measurement, making it impossible to precisely determine the moment the particle crosses the Rindler horizon.
These examples highlight the complexities and paradoxes that arise when quantum mechanics and relativity intersect, especially under extreme conditions. Understanding these phenomena in their entirety requires a unified theory of quantum gravity, an area that remains one of the most profound challenges in modern physics.
[3] Gültekin, K. (2023). Bose-Einstein condensation and black holes in dark matter and dark energy (Doctoral dissertation, İzmir Institute of Technology). İzmir, Turkey.