Continuous Time Crystals (CTCs) represent a fascinating new phase of matter that defies conventional expectations. Unlike discrete time crystals (DTCs), which require external periodic driving to exhibit time-translation symmetry breaking, CTCs spontaneously break continuous time-translation symmetry in an autonomous manner. This distinguishes CTCs from DTCs, as CTCs maintain their oscillations without any external driving force [Greilich et al., 2023; Kongkhambut et al., 2022; Kongkhambut et al., 2024]. Unlike ordinary crystals, which exhibit regular patterns in space, CTCs display periodic behavior in time, spontaneously breaking continuous time-translation symmetry manifesting a unique temporal order.
How Do Continuous Time Crystals Work?
The concept of time crystals was initially proposed by Nobel laureate Frank Wilczek as a way to extend the idea of spatial periodicity into the temporal dimension in thermal equilibrium. In Continuous Time Crystals, researchers turned to non-equilibrium systems, where periodic driving or environmental coupling allows for the emergence of time crystals [Xiang et al., 2024; Kongkhambut et al., 2022].
In Continuous Time Crystals, the symmetry breaking happens autonomously, without the need for an external periodic force. For instance, in specially designed electron-nuclear spin systems, CTCs have been observed to persist for hours. Here, the interplay between electron and nuclear spins, driven by continuous optical pumping, generates a self-sustained rhythm, a steady clocklike behavior that shows resilience across a range of conditions like temperature and magnetic field variations [Greilich et al., 2023; Kongkhambut et al., 2022].
Key Experimental Breakthroughs
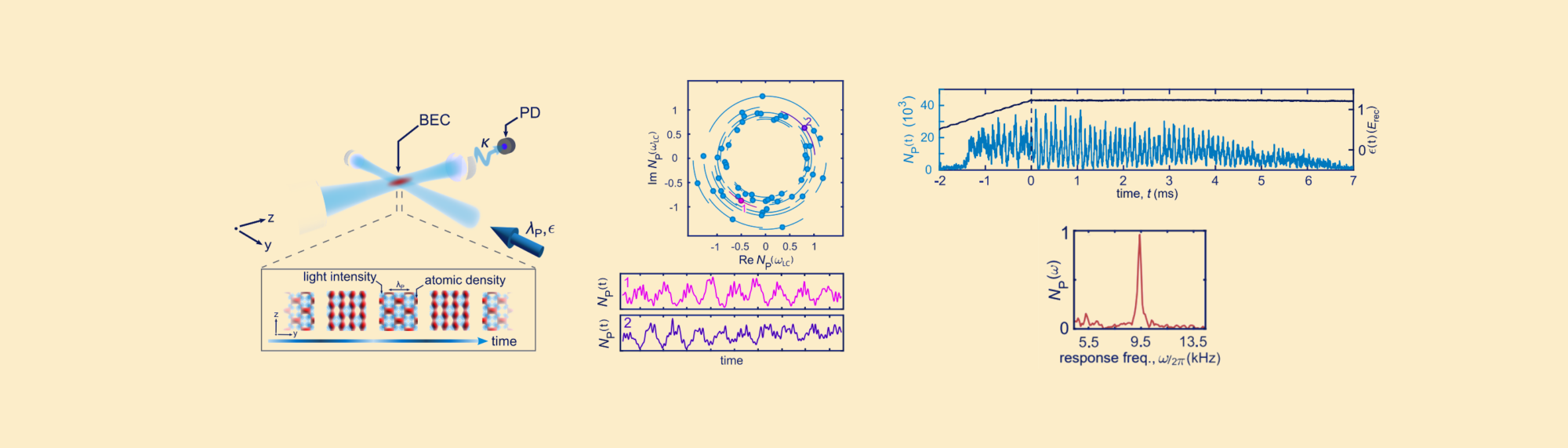
Recent experiments have further pushed the boundaries of understanding CTCs. In a notable study, a continuous time crystal was observed in a continuously pumped, dissipative atom-cavity system. This experiment used a Bose-Einstein condensate (BEC) of Rubidium-87 atoms inside a high-finesse optical cavity, transversely pumped with an optical field. The phase of the emergent oscillations was found to be random for different experimental realizations, signifying the spontaneous breaking of continuous time-translation symmetry. The observed robustness of these limit cycles against temporal perturbations confirmed the realization of a CTC [Kongkhambut et al., 2022].
One of the major experimental breakthroughs in this field came from the realization of a CTC in a semiconductor system. Scientists used a tailored InGaAs epilayer, continuously pumped with polarized laser light, to induce oscillations in the electron-nuclear spin dynamics. This system demonstrated an exceptionally stable time crystal, with coherence lasting hours, a first for solid-state systems. Remarkably, this stability allowed researchers to explore not only the regular oscillatory phase but also chaotic behaviors, which could be interpreted as the “melting” of the time crystal [Greilich et al., 2023].
Another important area of study involves the synchronization behaviors of CTCs. When multiple CTCs are coupled, they can enter exotic synchronization regimes such as chimera states, where some regions synchronize while others do not. This fascinating mix of order and disorder provides new insights into how time crystals might interact in complex networks [Solanki et al., 2024].
From Continuous to Discrete: Phase Transitions
Continuous Time Crystals can also transition into Discrete Time Crystals (DTCs). In an intriguing study, researchers modulated a CTC in an atom-cavity setup to induce this phase transition. By modulating the intensity of the pump, the CTC was locked to a subharmonic frequency, effectively transforming it into a DTC. This behavior is similar to phenomena like subharmonic injection locking, seen in non-linear systems such as lasers and mechanical oscillators [Kongkhambut et al., 2024; Kongkhambut et al., 2022].
CTCs Without External Driving
Recent work also showed that CTCs could be realized without relying on any periodic external driving, using purely dissipative quantum systems. In a continuously pumped atom-cavity system, the formation of a limit cycle phase represented the spontaneous breaking of continuous time-translation symmetry, an important hallmark of CTCs. The experimental results showed that this phase was stable against fluctuations, including quantum noise, suggesting a robust realization of a CTC in an open quantum system [Kongkhambut et al., 2022].
Typically, most time crystal realizations rely on external periodic driving, but a particularly exciting breakthrough showed that CTCs could emerge in purely dissipative systems without external drives. In these systems, dissipation alone, a normally disruptive influence, was enough to create sustained, periodic oscillations. Such CTCs were shown to be remarkably immune to heating effects, highlighting new possibilities for robust, non-driven time crystals that could operate without constant external input [Yang et al., 2024; Kongkhambut et al., 2022].
Spontaneous Symmetry Breaking and Random Phases
The concept of spontaneous symmetry breaking is crucial to understanding CTCs. Essentially, although the underlying physical laws of the system remain unchanged, the system itself chooses a specific state that breaks the inherent symmetry of those laws. In CTCs, this results in stable, continuous oscillations that emerge at arbitrary times, resulting in random initial phases for each cycle. This randomness in phase is a critical feature of CTCs and is indicative of the complex interplay between system dynamics and initial fluctuations [Tang et al., 2024].
Feedback and Retarded Interactions
Another important realization of a CTC involves an atom-cavity setup where a Bose-Einstein condensate was used. In this experiment, the system demonstrated self-sustained oscillations characterized by a limit cycle phase. The interaction between the pump lattice potential and the cavity-induced coupling led to a persistent oscillation of the intracavity intensity and atomic density, fulfilling the criteria for CTC formation. This experiment highlights how retarded interactions in an open quantum system can effectively induce time-crystalline behavior, circumventing the limitations posed by earlier no-go theorems [Kongkhambut et al., 2022].
Another exciting approach to realizing CTCs is through feedback-induced interactions. In hybrid spin maser systems, researchers introduced time-delayed feedback, effectively creating a retarded interaction that led to a stable, self-sustained oscillation. This setup brought CTCs even closer to the original idea of crystals, wherein interactions determine the structure. Here, the delayed feedback served as a temporal analog to the spatial lattice constant, reinforcing the idea of temporal periodicity without the need for conventional driving mechanisms [Wang et al., 2024].
The Future of Continuous Time Crystals
Continuous Time Crystals are more than just a theoretical curiosity, they open a window into new types of non-equilibrium phases and quantum technologies. From understanding fundamental quantum mechanics to exploring potential applications in quantum computing and sensing, CTCs have the potential to transform our approach to studying time-dependent phenomena. The robust oscillations and phase transitions in CTCs could offer new ways to build stable quantum systems that leverage temporal coherence, ultimately pushing the boundaries of what’s possible in quantum technology [Xiang et al., 2024].
Whether exploring self-sustained oscillations or the spontaneous emergence of order in non-driven systems, Continuous Time Crystals stand as one of the most compelling frontiers in modern physics, a testament to the rich tapestry of behaviors that matter can exhibit when freed from the constraints of equilibrium.
References
Kongkhambut, P., Skulte, J., Mathey, L., Cosme, J. G., Hemmerich, A., & Keßler, H. (2022). Observation of a continuous time crystal. Science, 377(6606), 670-673. Available at: arXiv version.
Greilich, A., et al. (2023). Continuous time crystal in an electron-nuclear spin system: stability and melting of periodic auto-oscillations. arXiv preprint.
Solanki, M., et al. (2024). Exotic synchronization in continuous time crystals outside the symmetric subspace. arXiv preprint.
Kongkhambut, P., Skulte, J., Mathey, L., Cosme, J. G., Hemmerich, A., & Keßler, H. (2024). Observation of a phase transition from a continuous to a discrete time crystal. Reports on Progress in Physics, 87(8), 080502. Available at: arXiv version.
Yang, X., et al. (2024). Emergent continuous time crystal in dissipative quantum spin system without driving. arXiv preprint.
Wang, Y., et al. (2024). Observation of continuous time crystal in a spin maser system. arXiv preprint.
Tang, Z., et al. (2024). Revealing spontaneous symmetry breaking in continuous time crystals. arXiv preprint.
Xiang, Y.-X., Lei, Q.-L., Bai, Z., & Ma, Y.-Q. (2024). Self-organized time crystal in driven-dissipative quantum system. Physical Review Research, 6, 033185. Published 19 August 2024. Available also at: arXiv version.