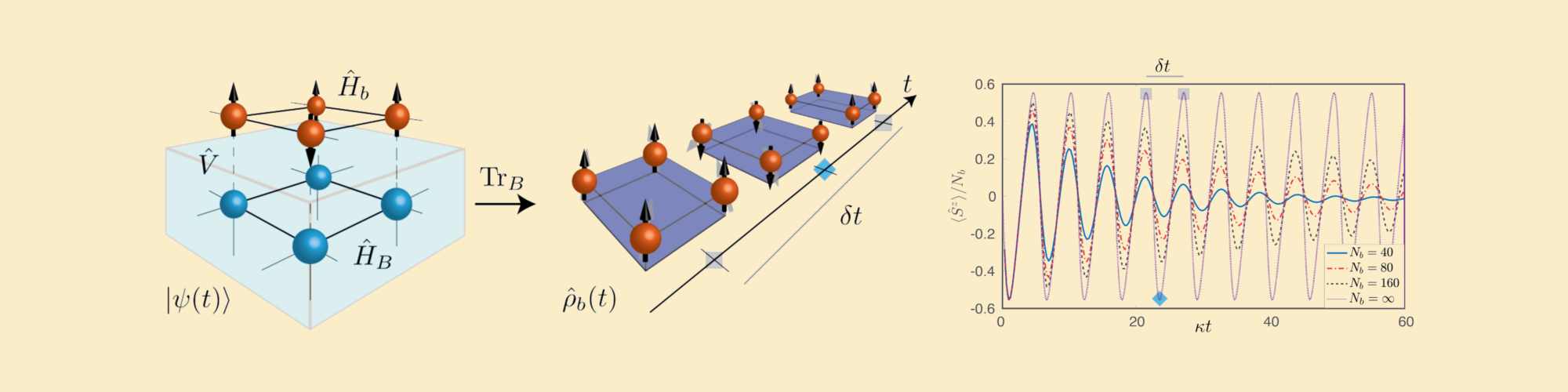
Boundary Time Crystals (BTCs) represent an exciting class of time-crystalline phases that form under non-equilibrium conditions, distinguished by their unique occurrence at the boundary of quantum systems. Unlike typical time crystals, BTCs manifest in a fraction of a many-body system, leading to a localized breaking of time-translation symmetry, while the rest of the system remains time-translationally invariant. This phenomenon makes BTCs fundamentally different from the typical bulk time crystals and has significant implications for their behavior and applications [Iemini et al., 2018; Carollo et al., 2024].
What are Boundary Time Crystals?
Boundary Time Crystals are quantum many-body systems where spontaneous time-translation symmetry breaking occurs at the boundary, rather than throughout the entire system. The system can be thought of as having two parts: the bulk and the boundary, each interacting through an interaction term. The BTC forms at the boundary, displaying persistent oscillations in the thermodynamic limit, even as the bulk remains in a time-independent state [Iemini et al., 2018]. This selective symmetry breaking is similar to the concept of surface critical phenomena, where only the surface layer shows ordered behavior.
The existence of BTCs is linked to the emergence of a time-periodic steady state in the thermodynamic limit of an open quantum system. The breaking of continuous time-translation symmetry leads to a self-organized, periodic pattern at the boundary, dependent on the system’s coupling constants [Iemini et al., 2018]. This unique behavior underlies the boundary’s persistent, macroscopic order, which forms despite the rest of the system remaining disordered.
Models and Dynamics of BTCs
A BTC can be modeled by considering a quantum many-body system in contact with an environment. For instance, a collection of two-level systems (spins) is collectively coupled to an external field, undergoing coherent driving and dissipative processes. This interplay creates conditions where only the boundary exhibits time-crystalline behavior. The Lindblad master equation is often used to describe the evolution of the system, where the collective dissipation and coherent driving compete to create the oscillatory phase characteristic of BTCs [Iemini et al., 2018; dos Prazeres et al., 2021].
Recent studies of BTCs have shown their robustness and versatility in different configurations of multi-level quantum systems. For example, in collective three-level systems, BTCs can exhibit more complex dynamics, such as the coexistence of multiple limit-cycles and chaotic behavior. In these systems, the BTC phase can be more resilient to perturbations compared to simpler two-level models, highlighting the diverse potential of BTCs as a new class of time-crystalline phases [dos Prazeres et al., 2021].
Applications and Sensing Capabilities
One of the most promising aspects of BTCs lies in their potential for sensing applications. Due to the interplay between coherent driving and dissipation, BTCs can be used for quantum sensing, especially in the presence of fluctuating external fields. The oscillatory phase of a BTC has been found to enhance sensitivity, achieving scaling that follows the standard quantum limit in time and the Heisenberg scaling in the number of particles, thereby providing an efficient means for parameter estimation [Cabot et al., 2024].
For instance, by continuously monitoring the quantum trajectories of a BTC, the sensitivity to external parameters can be maximized, making BTCs a powerful tool for sensing. Cascading two BTCs, where one serves as an input for the other, has been demonstrated as a method to surpass the standard quantum limit, revealing a pathway to even higher precision in sensing protocols [Cabot et al., 2024].
Quantum Thermodynamics of BTCs
The thermodynamic properties of BTCs add another layer of complexity and opportunity. BTCs operate in a genuinely non-equilibrium setting, where traditional thermodynamic descriptions do not fully apply. Studies have shown that BTCs remain stable even at finite temperatures, and their thermodynamic properties, such as heat currents, power exchange, and entropy production, display non-analytic behavior across phase transitions [Carollo et al., 2024].
A key finding in the quantum thermodynamics of BTCs is that these systems are robust to thermal effects and can maintain their time-crystalline phase even in high-temperature environments. This robustness makes BTCs attractive for practical applications, where maintaining coherence in noisy environments is often challenging. Furthermore, the link between thermodynamic quantities and collective magnetization operators suggests that BTCs could serve as a resource for quantum thermodynamic engines, pushing the boundaries of non-equilibrium quantum thermodynamics [Carollo et al., 2024].
The Future of Boundary Time Crystals
Boundary Time Crystals represent a significant expansion of our understanding of time-crystalline phases. They offer a novel perspective on how non-equilibrium conditions can lead to new phases of matter, specifically at the boundaries of quantum systems. With their unique properties and potential for applications in quantum sensing and thermodynamics, BTCs are poised to become a key focus of research in the coming years. Their ability to exhibit rich dynamics, from limit-cycles to chaotic behavior, and their robustness under various conditions, make them a fascinating subject of study for advancing both theoretical and applied quantum physics.
As research continues, the exploration of BTCs in different quantum systems and their integration into quantum technologies will likely unveil new possibilities for harnessing time-translation symmetry breaking in practical applications. From improving sensor precision to powering quantum devices, BTCs hold the promise of transforming our approach to quantum systems operating out of equilibrium.
References
Cabot, A., et al. (2024). Quantum sensing using boundary time crystals. Quantum Science and Technology, 9(035024).
Carollo, F., Lesanovsky, I., Antezza, M., & De Chiara, G. (2024). Quantum thermodynamics of boundary time-crystals. Quantum Science and Technology, 9(3), 035024. Published 7 May 2024.
dos Prazeres, L. F., Silva Souza, L., & Iemini, F. (2021). Boundary time crystals in collective d-level systems. Physical Review B, 103, 184308. Also available at: arXiv version. Published 20 May 2021.
Iemini, F., Russomanno, A., Keeling, J., Schirò, M., Dalmonte, M., & Fazio, R. (2018). Boundary time crystals. Physical Review Letters, 121(035301). Also available at: arXiv version. Published 16 July 2018.