Photonic Time Crystal PTC

Photonic Time Crystals (PTCs) are spatially homogeneous media whose electromagnetic susceptibility varies periodically in time, causing temporal reflections and refractions for any wave propagating within the medium.

1. Introduction to Photonic Time Crystals
   Photonic time crystals (PTCs) represent a revolutionary concept in the field of photonics, where the refractive index of materials is modulated in time rather than in space. This temporal modulation introduces momentum bandgaps, within which waves can experience exponential amplification, extracting energy from the time modulation itself. Unlike spatial photonic crystals that create energy bandgaps to filter specific frequencies of light, PTCs manipulate the momentum of electromagnetic waves, enabling novel behaviors such as non-resonant light amplification and tunable lasing. This groundbreaking approach offers a new dimension of control over light-matter interactions, with potential applications ranging from quantum optics to advanced photonic devices​ . Recent studies also explore polariton-exciton condensates—hybrid light-matter quasiparticles formed through strong coupling between photons and excitons in semiconductor microcavities. These polaritons exhibit superfluidity and coherence, making them a promising candidate for neuromorphic computing ​.
2. Materials Enabling Rapid Refractive Index Modulation
   One of the key challenges in realizing PTCs at optical frequencies lies in achieving significant and rapid refractive index changes within ultra-short time scales. Conventional materials and nonlinear optics approaches, such as photorefractive effects or thermal nonlinearities, are too slow or weak for PTC implementation. Recent advances in materials science, however, have identified promising candidates, including transparent conducting oxides (TCOs) and phase-change materials, that offer large refractive index modulations in the required femtosecond timescale. These materials, especially those operating near the epsilon-near-zero (ENZ) regime, have shown the potential to achieve the sharp transitions needed for PTCs, marking significant progress toward practical implementations . Polariton-exciton condensates leverage the strong coupling of light and matter, enabling picosecond-scale reaction times, ideal for high-speed photonic applications. In neuromorphic systems, polariton lattices create binary neuromorphic networks, where each “neuron” (represented by a polariton condensate) performs binary operations. This design improves computational efficiency and scalability​ .
3. Momentum Bandgaps and Non-Resonant Amplification
   At the core of PTCs is the formation of momentum bandgaps, regions in momentum space where no propagating wave solutions exist. Waves entering these bandgaps are exponentially amplified, drawing energy from the time modulation of the material. A similar phenomenon has been observed in polariton condensates, where nonequilibrium phase transitions in optically trapped systems lead to spatially and temporally ordered phases, akin to semiclassical time crystals. These condensates exhibit spontaneous temporal periodicity, which can be detected through frequency combs in the polariton lasing spectrum, highlighting their potential for non-resonant gain and wide-band amplification . This effect, unlike traditional resonant amplification in optical systems, does not require phase matching or specific resonant conditions, allowing for non-resonant gain. This makes PTCs highly versatile for applications that require wide-band amplification, and it opens the door to innovations such as thresholdless lasing and the amplification of phonons, further extending the possibilities of this technology . This is analogous to polariton lattices, which employ the spatial coherence of coupled condensates to create binary neurons that operate in a similar binary fashion. The polaritons’ nonlinear behavior enables efficient parallel processing, significantly enhancing computational speed, as demonstrated in binary neuromorphic networks that leverage polariton lattices for complex operations like handwritten digit recognition with up to 97.5% accuracy .
4. Experimental Demonstrations and Practical Implications
   Recent experimental demonstrations of PTCs have shown their practical viability, particularly in the microwave regime. Similarly, polariton-based systems have shown great promise for applications like neuromorphic computing. In these systems, time crystals—structures that exhibit periodicity in time rather than space—could be integrated to enhance temporal processing and memory functions within neuromorphic networks​ . For instance, researchers have observed time-reflection and broadband frequency translation in transmission-line metamaterials. These experiments prove the ability of PTCs to manipulate waves not just in space but also in time, with implications for photon control in both classical and quantum regimes. The concept of a temporal Fabry-Perot cavity, formed by combining multiple time interfaces, demonstrates the potential for extreme wave manipulation, laying the groundwork for future developments in time-metamaterials and Floquet systems .
5. Future Prospects of Photonic Time Crystals
   The rapid advancements in both the theoretical and experimental understanding of PTCs highlight their potential to transform multiple fields of photonics. From enabling non-resonant amplification to supporting quantum light-matter interactions, PTCs provide new ways to control light across space and time. As material science continues to push the boundaries of what is possible in terms of modulation speed and depth, we can expect further breakthroughs in the realization of optical PTCs. With continued exploration of novel materials and techniques to overcome power and speed constraints, PTCs are poised to unlock new frontiers in photonic applications . Additionally, the development of polariton condensates as semiclassical time crystals offers another avenue for realizing PTCs. Additionally, neuromorphic networks based on polariton condensates present a novel architecture where binary neurons offer efficiency and scalability benefits for tasks like pattern recognition and data processing . These condensates exhibit spontaneous formation of high angular momentum quantum vortices in optically induced traps, enabling new forms of light manipulation and potential breakthroughs in quantum photonics .

Temporal Modulation

The defining feature of PTCs is their time-dependent electromagnetic susceptibility. This means that the material’s response to an electromagnetic wave (such as its refractive index or dielectric constant) changes periodically over time. These temporal changes are analogous to the periodic spatial variations seen in regular photonic crystals but occur in the time domain.

Homogeneous in Space

Unlike conventional photonic crystals, which are made of different materials or structures arranged in a periodic pattern in space (such as a grid of rods or layers of different materials), PTCs are spatially uniform. The periodicity is entirely in the time domain, meaning the material looks the same at any point in space at a given time but changes its properties as time progresses.

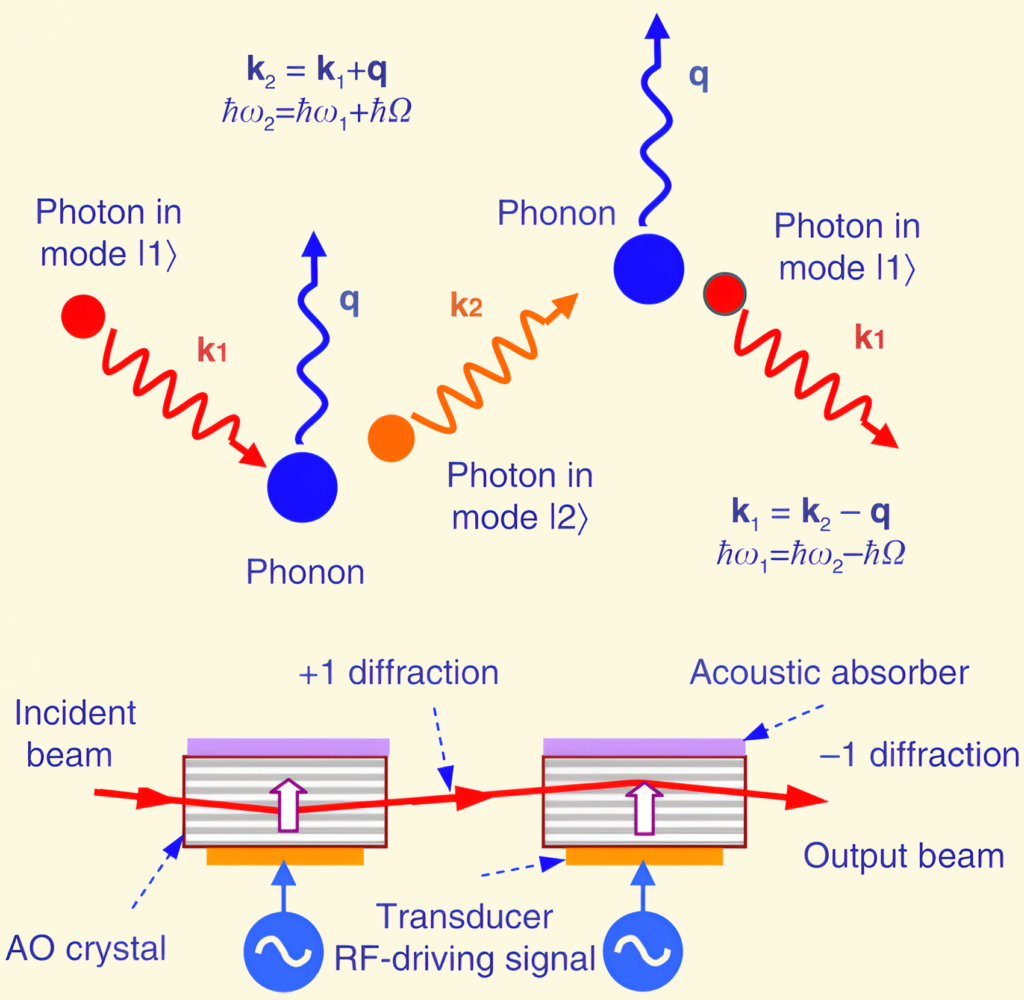
Photon Phonon Crystals

In a phonon-photon time crystal, both light (photons) and lattice vibrations (phonons) are influenced by a time-periodic structure. The interactions between photons and phonons can lead to non-reciprocal effects and other complex behaviors, as described in the document regarding the photonic Aharonov–Bohm effect, where both phonons and photons exhibit time-crystal-like behavior .

Phonon Photon Time Crystals

Longitudinal Optical Phonons in Photonic Time Crystals
Photonic time crystals also hold potential for amplifying longitudinal optical phonons, as demonstrated in Lorentzian medium-based dispersive PTCs. A stationary charge embedded in such PTCs can excite these phonons through the static polarization field it induces. The PTCs can develop an infinite momentum bandgap across the entire wave vector space, enabling exponential amplification of the longitudinal modes. This amplification can be achieved with minimal refractive index modulation, making it a practical method for exploring momentum bandgap phenomena in realistic optical experiments. The unique interaction between stationary charges and longitudinal phonons in PTCs extends the range of waves that can be manipulated and offers new opportunities in time-varying photonics​ .

Experimental research on optically trapped polariton condensates reveals their potential as semiclassical time crystals. These systems break time translation symmetry through spontaneous phase transitions, resulting in spatially and temporally ordered condensates. This dynamic interaction between polaritons and excitons in such systems closely mirrors the behavior of PTCs and could lead to new methods for amplifying both photon and phonon interactions, further expanding the range of waves that can be controlled in time-varying photonic systems .