A Fusion of Twistor String Theory and Time Crystals
The “Twistor String Time Crystal” concept merges the intricate geometry of twistor string theory with the groundbreaking physics of time crystals. By combining these two advanced theoretical frameworks, this idea opens up new possibilities for understanding quantum phenomena and exploring novel states of matter.
What is Twistor String Theory?
Twistor string theory, introduced by Edward Witten in 2003, is a theoretical physics framework that integrates twistor theory with string theory. At its core, twistor theory offers a unique geometric perspective for describing spacetime, while string theory provides a unifying description of fundamental particles and forces. Together, twistor string theory has been instrumental in simplifying calculations of scattering amplitudes in quantum field theory, particularly in elementary particle physics. This elegant mathematical approach relies on the geometry of twistor space, a higher-dimensional representation that simplifies complex interactions.
For more about twistor string theory, visit:
Twistor String Theory on Wikipedia
Foundations in Twistor Theory: Frequency Splitting and Helicity Frameworks
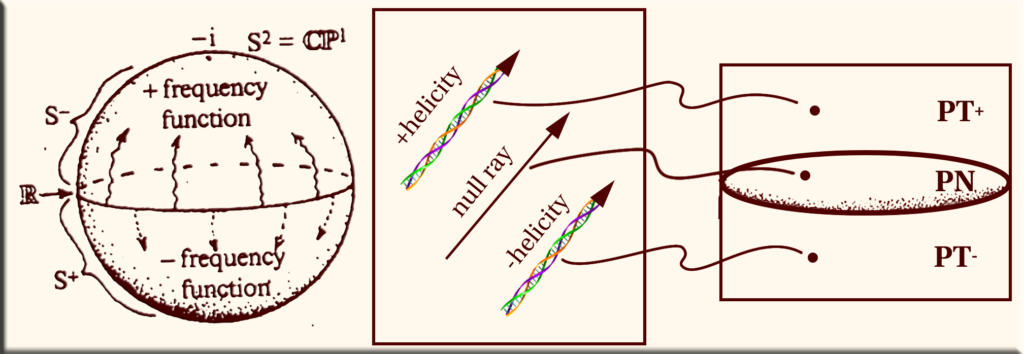
S² = CP¹: This represents the Riemann sphere or complex projective line (CP¹). In twistor theory, the Riemann sphere often represents a space where certain mathematical transformations and mappings occur.
S⁺ and S⁻: positive frequency (S⁺) and negative frequency (S⁻) components. These are associated with the decomposition of waves or fields in physics.
+helicity / -helicity: helicity of particles, which describes the projection of a particle’s spin onto its momentum direction. Positive helicity (+) indicates the spin is aligned with momentum, and negative helicity (-) means the spin is opposite to the momentum.
PT⁺, PT⁻, and PN: twistor space components, where PT⁺ is Positive twistor space, PT⁻ is Negative twistor space, and PN the null twistor region or projective null space, an intermediate state or a transition space between the positive and negative components.
Riemann Sphere Representation
Using the Riemann sphere to compactify the complex plane, time is represented as the equator, with the northern and southern hemispheres corresponding to positive and negative frequencies, respectively. This conformally invariant splitting was extended beyond one-dimensional time to Minkowski spacetime.
Challenges with Minkowski Space
The challenge arose when the complexified Minkowski space could not be naturally divided into two halves. The solution was found by focusing on the space of light rays rather than spacetime itself. In this approach, points in spacetime are represented by the family of light rays passing through them, and the celestial sphere, inherently complex and conformally invariant, represents the space of light rays.
Helicity Framework in Twistor Space
This led to the conceptual framework of Twistor space, which divides into two halves: the top half corresponds to positive helicity (e.g., right-handed massless particles), and the bottom half to negative helicity. Geometrically, this involves stereographic projections and Clifford parallels of a three-sphere, visualizing the intricate relationships within Twistor Theory.
For the latest research, see:
Time Crystals on arXiv
Twistor String Time Crystal: A New Paradigm
Recent advancements in the simulation of quantum time crystals highlight how such systems can be arranged in frequency space, enabling novel approaches to understanding quantum dynamics.

By integrating the concepts of twistor string theory and time crystals, the Twistor String Time Crystal represents a potential breakthrough in quantum physics. This combination allows for:
- Geometric Representation of Temporal Periodicity: Twistor space provides an elegant mathematical tool to describe the periodic motion of time crystals, potentially simplifying the study of systems that break translational-time symmetry.
- New Approaches to Quantum Simulation: The frequency-space arrangement of time crystals can be further explored through the lens of twistor geometry, leading to insights into non-equilibrium quantum states.
- Applications in Quantum Field Theories: By leveraging twistor string theory’s ability to calculate scattering amplitudes, researchers can investigate how periodic quantum systems behave during particle interactions.
The Twistor String Time Crystal has applications in advancing quantum computing and quantum computers. Integrating these concepts supports the development of quantum technologies, enabling research into the stability of quantum states and their potential use in computations.
Why It Matters
The Twistor String Time Crystal concept bridges the gap between two seemingly disparate areas of physics. It offers a novel framework to explore quantum coherence, time symmetry-breaking phenomena, and advanced geometrical representations of quantum states. This multidisciplinary approach has the potential to inspire new experimental setups and deepen our understanding of the quantum universe.
For further foundational reading:
- “Twistor String Theory and Particle Physics” on ScienceDirect
- Frank Wilczek’s Proposal of Time Crystals
Exploring the Future
The Twistor String Time Crystal is a frontier at the intersection of mathematics, quantum field theory, and condensed matter physics. As research progresses, this concept paves the way for breakthroughs in quantum computing, particle physics, time, and frequeny space.

